Particle Tracking

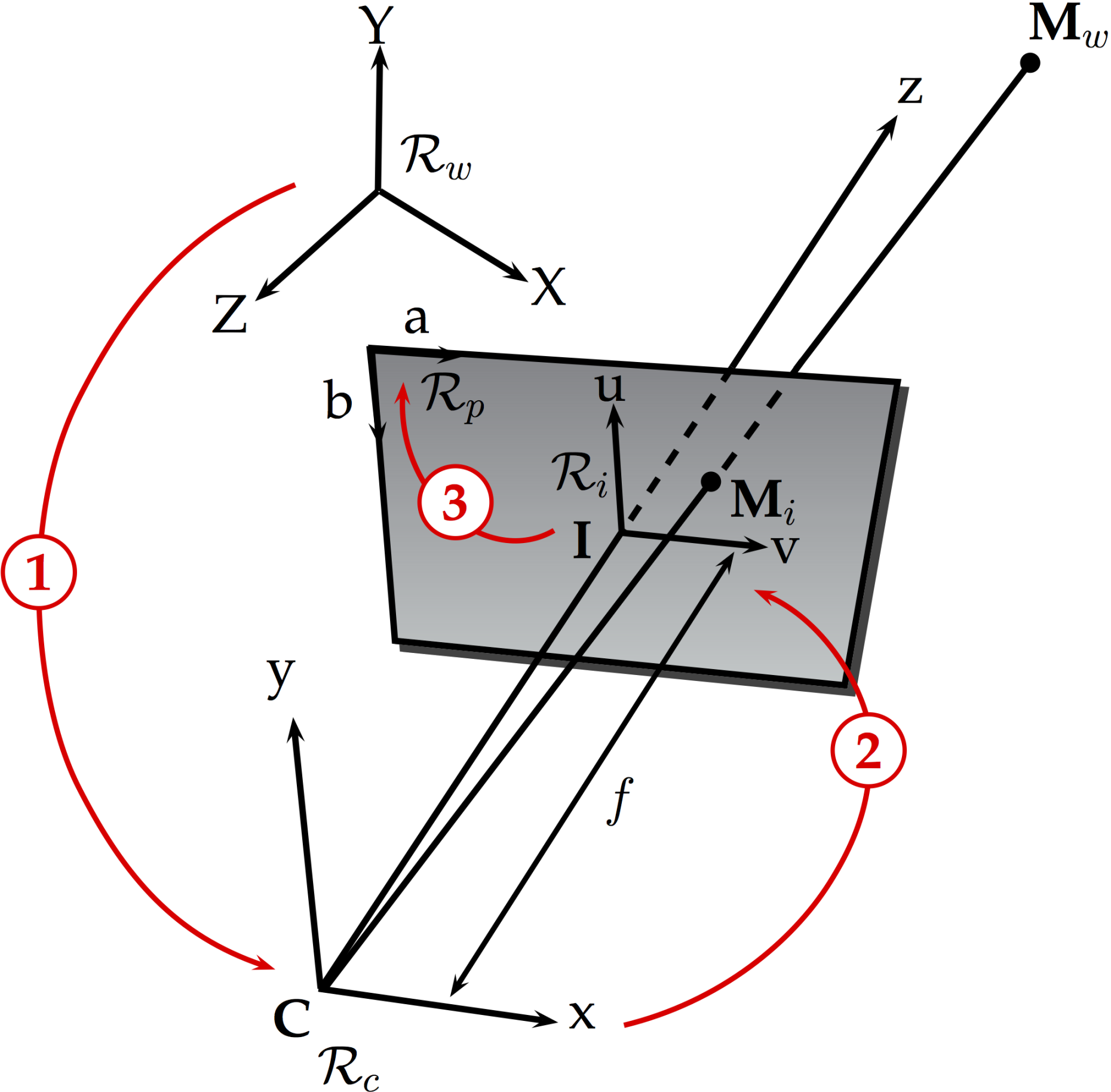
Pinhole camera model

This method is based on the pinhole camera model, which is an approximation of the relationship between a point M_w in the world reference frame and its projection M_i onto the focal plane of the camera and finally onto the point M_p in the final image. In this model, the coordinates of M_w and M_p are related by a set of extrinsic and intrinsic camera parameters. Extrinsic parameters define the location and orientation of the camera reference frame with respect to the known world reference frame, and are represented by the translation vector between the relative positions of the two frames and the rotation matrix which brings the corresponding axes into alignment. Intrinsic camera parameters are required to link the point M_w expressed in the camera reference frame with the coordinates of its corresponding point M_p. A perspective projection links the coordinates of M_w to the point M_i in the image plane. A second transformation describes the sampling of the focal plane by the camera sensor and links the coordinates of M_i to the coordinates of M_p. The combination of these three transformations gives the collinearity equations. The basic pinhole model is then extended with some corrections for radial and tangential distortions. The camera model becomes non-linear and can be expressed as a vectorial function which is suited to be linearized as observation equations. Finally a radial shift is calculated and added into the collinearity equations to compensate for the influence of the multimedia geometry (Maas et al. 1993).

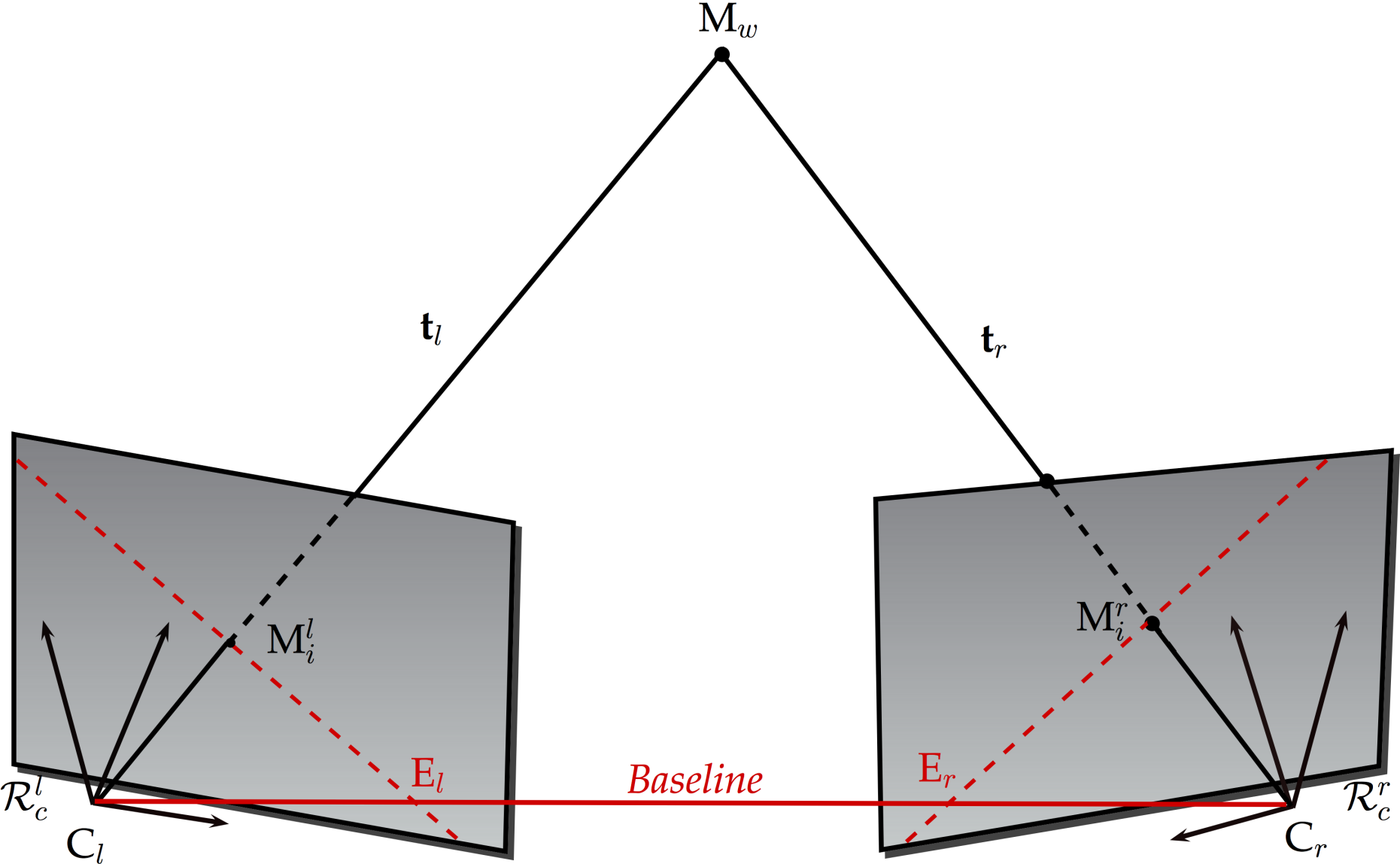
Epipolar geometry

The extended pinhole model is being applied for a spatial resection using control points with known coordinates and introducing the parameters of exterior and interior orientation, lens distortion and sensor distortion as unknowns (Maas et al., 1993). Knowing the camera orientation and parameters, it is then possible to establish correspondences between particle image coordinates. A point in the world reference frame is projected onto both image planes to points constituting a conjugate pair. For a point in the left image plane, its conjugate in the right image plane lies on a line called the epipolar line. An essential matrix expresses the relation between these two points. Given a point in one image plane, multiplying its coordinates by the essential matrix will determine which epipolar line to search along in the second image plane. After corresponding particles on the two images are found, the three-dimensional coordinates are derived by forward intersection, introducing their coordinates as unknowns in the augmented projection model (Papantoniou and Dracos 1989; Maas et al. 1993; Malik et al. 1993; Dold and Maas 1994).

Particle tracking

Particles are detected within images by the application of a peak-fitting routine after high-pass filtering, and their center of gravity is calculated with a weighted gray value operator (Maas et al. 1993). The corresponding particle coordinates in the object space form the point clouds at each time instant before the tracking is performed (Willneff, 2003). The tracking procedure then selects correct links for the individual particle from one time step to the next, using the information extracted from both image and object spaces (Dracos 1996; Willneff 2003). If a particle can be tracked in the object space over several consecutive time steps, its position in the next time step can be predicted assuming constant velocity or constant acceleration and back-projected onto the images of all cameras. The search in the image space after projection of the search volume from the object space either confirms the predicted location or leads to unmatched detections.